The Top Ten Martin Gardner Scientific American Articles

The "Mathematical Games" column in Scientific American that began in January 1957 is a legend in publishing, even though it's almost thirty years since the last one appeared. They are still considered models of clarity and elegance in introducing fresh and engaging ideas in mathematics in non-technical ways.

As we pause to celebrate the centennial of the man who wrote them, the ever-prolific Martin Gardner (1914–2010), we note that while many of his articles fell under the umbrella of "recreational mathematics", others touched on cutting-edge new concepts involving contributions from some of the world's most creative minds. Even the articles that initially seemed to be purely for entertainment sometimes gave rise to research with serious ramifications later on. And some of the ideas had a big impact in the real world too. It's all the more remarkable considering that Martin had no formal training in mathematics.

In his memoirs Undiluted Hocus-Pocus (Princeton, 2013), Martin recalls,

"One of the pleasures in writing the column was that it introduced me to so many top mathematicians, which of course I was not. Their contributions to my column were far superior to anything I could write, and were a major reason for the column’s growing popularity. The secret of its success was a direct result of my ignorance. Even today my knowledge of math extends only through calculus, and even calculus I only dimly comprehend. As a result, I had to struggle to understand what I wrote, and this helped me write in ways that others could understand.

How does one decide on the top ten Martin Gardner Scientific American articles, from the roughly 300 that he wrote for the magazine? The vast majority of those were "Mathematical Games" columns, which appeared monthly from January 1957 and December 1980, then increasingly sparodically until June 1986. Should we focus on the ones that are most talked about today, or the ones that generated the biggest volume of correspondence upon pubication? Or the articles which seem to have spurred more developments or real research than any of the others? The list that follows reflects all of those considerations.

Including the "first" Scientific American article "Flexagons" from December 1956 is a no-brainer. It was actually the second piece Martin wrote for the magazine—"Logic Machines" had appeared as a one-off back in March 1952—but it promptly resulted in an invitation to write a monthly column. Thus, in January 1957, "Mathematical Games" proper was born.

Likewise, the columns introducing readers to the art of M. C. Escher and Mandelbrot's fractals are hard to ignore, as is the infamous April Fool one. In 1993, Martin himself identified the columns on Sol Golomb’s polyomino results, John Horton Conway’s Game of Life, Newcomb’s paradox, Penrose tiles, and RSA cryptography as the ones he remembered as having generated the most reader response. If we add these to the first four selected, it seems that we already have nine of the Ten Top articles nailed down. There are others clamoring for attention, such as the columns on the Soma cube, rep-Tiles, the unexpected hanging, hypercubes, or packing spheres, but let's look elsewhere for our final selection.

One popular recurring feature of "Mathematical Games" was collections of short puzzles or brainteasers—generally nine in number—for which readers had to wait until the following month to see the solutions. Since many of the problems posed in these columns have achieved the status of classics, and are still excellent brain candy for the modern age, it seems appropriate to top off the list with one of these collections.

When Martin's Scientific American articles resurfaced later as chapter in books—especially the fifteen spin-off collections (issued between 1959 and 1997) that his friend computer science pioneer Donald Knuth refers to as "The Canon"—they were often expanded, with additional notes and updated lists of references. A few even spawned entire followup chapters, in cases where there had been considerable development in the field.

Below, we focus on the original pieces. Without further ado, we present, in order of publication, an annotated list of what are, in our opinion, The Top Ten Martin Gardner Scientific American Articles:

1. "Flexagons, in which strips of paper are used to make hexagonal figures with unusual properties" (December 1956).

Better known today as "Hexaflexagons," this piece was written as a standalone, but was such a hit with editor Gerry Piel (and, in due course, with readers), that Martin was invited to contribute a monthly column for the magazine. It started in January 1957, under the banner "Mathematical Games."

Hexaflexagons are hexagonal folded paper objects which can be transformed repeatedly by "turning them inside out" to reveal new faces. In his memoirs, recounts how he was introduced to them by Royal V. Heath—the man credited with popularizing the term "mathemagic" from 1951 onwards. Flexagons had been accidentally discovered in Princeton in 1939, by an English graduate student named Arthur Stone, and they were then explored mathematically by him and fellow students John Tukey, Bryant Tuckerman, and Richard Feynman. The war intervened, and paper curiosities were forgotten. It fell to Martin to revive them fifteen years later, little dreaming that it would launch him on the most successful phase of his career.

As he noted shortly before his death, "Today there are some fifty websites devoted to flexagon theory and variants of the original forms." Here are two from more recent times, that will guide you through making your own:

Hexaflexagon Templates (ours from 2012, a great deal of time and effort went into making this "perfect" so we hope you can list it!) and Make Your Own Hexaflexagons…and Snap Pictures of Them (Sci Am's, only does trihexaflexagons?)

2. "More about complex dominoes" (December 1957).

This is remembered today for introducing readers to mathematician Sol Golomb's five-square versions of "polyominoes"–pieces formed by fitting several unit squares together along their edges. As Martin notes in his memoirs, "A single square is the monomino, two squares are the dominoes, three the trominoes, four the tetrominoes, and five the pentominoes. The problem of finding a formula for the number of n-ominoes, given n, is still a deep unsolved combinatorial problem. My first column on Golomb’s twelve pentominoes was an instant hit. I returned to polyominoes in several later columns."

3. "A third collection of 'brain-teasers'" (August 1958).

Martin's regular compendiums of short head-scratchers forced readers to either buckle down and solve the problems therein, or wait a full month to see what solutions and comments the next column offered. The only "websearch" option available in the Sputnik and Apollo eras was to write to the man himself, which many people did, but those were usually readers with new solutions or fresh material to offer.

Surveying those special columns today, one is struck by how many gems they contain. The Returning Explorer (aka "one mile south, one mile east, one mile north"), The Mutilated Chessboard, The Fork in the Road (truth-tellers and liars), the mind-boggling Hole in the Sphere, and the "obvious once you get it" Touching Cigarettes. (Yet, there's an exciting new development in the last problem, as Martin's bibliographer and biographer Dana Richards recently reported.)

In the face of such tough competition it's not easy to select an outright winner here, but we selected "A third collection of 'brain-teasers'" from August 1958. It opens with the iconic Twiddled Bolts, depicted above, and continues with The Cork Plug, and The Sliding Pennies. For us, pride of place goes to The Colliding Missiles:

Two missiles speed directly towards each other, one at 9,000mph and the other at 21,000mph. They start 1,317 miles apart. Without using pencil and paper, calculate how far apart they are one minute before they crash.

Needless to say, one should not use a calculator, slide rule or abacus either! (Martin's son Jim reports that the last-named device was his dad's weapon of choice when balancing his check book.)

A tiny knowledge of physics helps, and we believe there is a profound moral hiding within this question's presentation. See the solution and comment at the very end below.

4. "Concerning the diversions in a new book on geometry" (April 1961).

This column, and its associated Scientific American cover, introduced many people to the pre-psychedelic creations of Dutch artist M. C. Escher. When it reappeared in later books, Martin's article was called "H. S. M. Coxeter," after the Toronto-based geometer whose book An Introduction to Geometry (Wiley, 1961) his column surveyed.

It's hard to believe today, but by the early 1960s geometry and visualization in mathematics had fallen out of favor, in deference to more abstract branches of the subject and more formal reasoning. Indeed, it was not unheard of for mathematics books to contain few if any pictures. This book, as Martin gleefully reported with wonderful accompanying images, revealed many delicious surprises, including Morley's Theorem, and the difficulty of proving the Internal Bisector Theorem. He then quotes "The Kiss Precise"—a verse immortalizing a curious result about any three mutually touching circles—before moving on to tesselations.

Escher's knights on horseback from Coxeter's book make an appearance, but the cover is a Scientific American exclusive, the now famous flying geese (which the art department colored without consulting the artist). As it happens, Escher was already a fan of Martin's, and in particular of his recent Annotated Alice (Potter, 1960).

5. "The fantastic combinations of John Conway's new solitaire game `life'" (October 1970)

Better known today as "Life" or "The Game of Life," this column ventured into very new territory as it explored a cellular automaton creation of English mathematician John Horton Conway. To quote Martin at the time, "Because of its analogies with the rise, fall and alterations of a society of living organisms, it belongs to a growing class of what are called "simulation games"–games that resemble real-life processes. To play Life without a computer you need a fairly large checkerboard and a plentiful supply of flat counters of two colors."

As it turned out, many people with then-rare access to mainframes seized the opportunity to program Life. But there was also great theoretical interest in the new game. Referring to the animation above, which was reported in a later column, Martin relayed in his memoirs that "Conway was the first to prove that Gosper’s glider gun turned Life into a Turing machine that in principle can do everything the most powerful computers can do."

He continued, "All over the world mathematicians with computers were writing Life programs. I heard about one mathematician who worked for a large corporation. He had a button concealed under his desk. If he was exploring Life, and someone from management entered the room, he would press the button and the machine would go back to working on some problem related to the company!" He also noted that his first column on Life "made Conway an instant celebrity. The game was written up in Time."

6. "Free will revisited, with a mind-bending prediction paradox by William Newcomb" (July 1973)

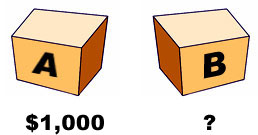
Better known today as "Newcomb's Paradox," this concerns a free will paradox devised by physicist William Newcomb in 1960, and then featured in a paper by philosopher Robert Nozick in 1970. Imagine two closed boxes, A and B, on a table. Box A is known for sure to contain $1,000, whereas Box B contains either nothing or $1,000,000, but you don't know which. Two courses of action are open to you: either take what is in both boxes, or take only what is in Box B.

Here's the catch: we are to believe that a superior Being has predicted in advance which choice you will make, and if (s)he predicts you will choose both boxes, (s)he has left Box B empty, otherwise (s)he has put $1,000,000 in it. Also, if (s)he expects you to flip a coin to decide on your course of action, (s)he has definitely left Box B empty.

Martin goes on to present very strong arguments why each course of action is superior to the other, using expected payoff value computations, and discusses both sides of the argument at length. He concludes, "Can it be that Newcomb's paradox validates free will by invalidating the possibility, in principle, of a predictor capable of guessing a person's choice between two equally rational actions with better than 50 percent accuracy?"

7. "Six sensational discoveries that somehow or another have escaped public attention" (April 1975)

This unprecedented April Fools prank column went over the heads of many readers. At a time when "new results" of any type could not be researched on the internet, calculators only displayed eight digits, and very few people had access to computers, Martin got away with the astonishing claim that

e^{𝛑 sqrt(163)} = 262,537,412,640,768,744.

simply because nobody could really check, and it seemed close to true to anyone who did a ballpark calculation! He attributing it to Indian mystic mathematician Ramanujan, which was a total red herring, but this "near miss" turns out to have mathematical significance.

He also revealed that the valve flush toilet was invented by Leonardo da Vinci, and had convincing looking drawings ("courtesy of N.Y. Public Library") to prove it; throwing in an account of related pattents by English plumbing fixture manufacturer Thomas Crapper. Then there was the announcement of a computer proof that in chess, the move "pawn to king's rook 4" is a win for white, "with a high degree of probability."

Most dramatically, he unveiled a 110-region map (shown above) which he said could not be colored with fewer than five colors. If true, this would have provided a counterexample to the then long-standing four-color-map conjecture. It certainly wasn't easy to color this parricular map with four colors. Martin's timing was impeccable: a year later Appel and Haken announced a "computer assisted" proof that all maps can indeed be four-colored. Their argument, which has stood the test of time, included showing that there is a particular set of 1,936 maps, each of which cannot be part of a smallest-sized counterexample. Coincidentally, Martin graduated from the University fo Chicago in 1936 (with a degree in philosophy).

From Martin's memoirs, "I received hundreds of letters showing how to color my map with four colors. Many readers, including a few scientists, thanked me for alerting them to such important discoveries but chided me for being totally mistaken about one of them."

8. "In which 'monster' curves force redefinition of the word `curve'" (December 1976)

(the pic we need here is "first three orders of Benoit Mandelbrot's square snowflake" from the original article)

Later known as "Mandelbrot's Fractals," this column begins by discussing the nature of what's been understood by the word "curve" throughout history, from ancient Greece to seventeenth century notions based on analytic geometry, and the concepts of continuity and differentiabily that the calculus age ushered in. Early examples of so-called pathological or monster curves, such as Koch snowflakes, are next, along with their unavoidable paradoxes. How can a curve fill the plane, or space, and how can the distance between two points on a curve be infinite?

Mandelbrot's formalization of a new type of dimension—which he named fractal dimension only a year or two before this column was published—is explained in terms of self-similarity at various scales. Examples covered include Bill Gosper's "flowsnake" curve, then brand new, Mandelbrot's own square snowflake, and Cantor dust.

Mandelbrot lived not far from Martin when this piece was written, and around this time, at his own home, Martin introduced him to Conway. As he relays in his memoirs, "Conway had been making new discoveries about Penrose tiling, and Mandelbrot was interested because Penrose tiling patterns are fractals. You can keep enlarging or diminishing them, always to obtain similar patterns."

Which leads us neatly us to our next article, which was published back to back with the one just discussed.

9. "Extraordinary nonperiodic tiling that enriches the theory of tiles" (January 1977)

Better known as "Penrose Tiling I"—the title under which it appeared in later books—this gave Martin another cover story, the cover artwork having been sketched by John Conway (and later colored by a Scientific American staff artist).

It starts with a survey of traditional tilings, such as those done with squares, dominoes, and hexagons, which are generally periodic. Martin then explains how many—but not all—of these are also associated with nonperiodic tilings. He draws on images of M. C. Escher and Sol Golomb (the latter's "reptiles"), before asking, "Are there any sets of tiles that tile only nonperiodically?" This leads to the fascinating story of Penrose's mid 1970s discovery of what are now known as Penrose tiles (or, darts and kites, following a suggestion of Conway's).

In his memoirs, Martin comments, "To Penrose’s vast surprise, it turned out that three-dimensional forms of his tiles would tile space only aperiodically! Not only that, but such shapes could actually be fabricated in laboratories. They became known as quasicrystals. Hundred of papers have since been published about them. They are a marvelous example of how a mathematical discovery, made with no inkling of its application to reality, may turn out to have been anticipated by Mother Nature!

In 2011, chemist Dan Shechtman was awarded a Nobel Prize for "the discovery of quasicrystals."

10. "A new kind of cipher that would take millions of years to break" (August 1977)

Later known as "Trapdoor Ciphers," this introduced RSA Cryptography, a new "public key" method of secret communication previously not believed possible. It was based on an MIT memo by Ron Rivest, Adi Shamir and Leonard Adleman, from April 1977, which they sent to Martin. He was so impressed that he broke his usual rule of planning his column several months in advance, and quickly wrote it up for publication.

The basic idea is to secretly take two very large prime numbers p, q, say at least 40 digits long each, and form their product r=pq, assuming that it would be an insurmountable task for an outsider to factor r. It's considered safe to reveal r, as well as a related odd number s, to all and sundry; that's the public key. Anyone wishing to send a secret numerical "word" w to the person who selected p and q does the following: find the remainder e when w^s is divided by r, and communicate e openly. An easy mathematical trick allows a person who knows e to reconstruct w from it provided they know the factors p and q of n, but it seems unlikely that somebody not knowing p and q would have a chance.

To prove the point, the RSA team provided Martin with a 128-digit coded message e, computed using a specified 129-digit n which was the product of mysterious top-secret 64-digit and 65-digit primes p and q, respectively. They also indicated that s = 9007. A prize of $100 was offered for anyone who could recover the original message w from which e had been computed. Given the title of the column, it was believed that no one would crack it anytime soon.

RSA cryptography became an industry standard, and variations of it are still in use today, though in recent times the question of how secure it is has been revisited. Despite the groundbreaking nature of Martin's column, it didn't quite live up to its title. The challenge message posed in it was sucessfully decoded as early as April 1994.

Apologies and Addendum

Opinions will of course vary on the items to include in any top ten list, and it's likely that many reader favorites are missing above. Apologies. We also regret any offense caused to fans of the late great Dr. Irving Joshua Matrix; none of his adventures made the final cut either. Maybe if the list went to 11...

In the introduction to The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems (W. W. Norton, 2001), Martin wrote that the book resulted from his editor suggesting that he "select 50 of what I consider my 'best' columns, mainly in the sense of arousing the greatest reader response []." Curiously, not all of the columns highighted in our Top Ten list above are to be found in that tome's 724 pages; he even omitted some of his own "top five" (from his 1993 comments refered to earlier).

There is no shortage of things to explore.

LINK TO THE NEW SCI AM STUFF, eBOOK ETC. and to the official Martin Gardner site

Solution and comment for The Colliding Missiles:

We may as well assume that one missile is stationary and the other is barrelling towards it at 30,000mph (their relative speed). Since distance traveled in this case is found by multiplying speed by time taken, it follows that in one minute, namely, is 1/60 of an hour, the moving missile travels (30,000) x (1/60) = 500 miles. That's how far apart the missiles must be a minute before they collide.

Most readers are surprised—and some feel disappointed or cheated—that we don't need the fact that the missiles started 1,317 miles apart. Does this make it an unfair, "trick" question? That depends on one's perspective. Consider this: in the real world, unlike in many textbook situations, we're bombarded with information and data. Learning to distinguish the essential from the irrelevant is a key skill worth acquiring. Once more, with this puzzler, rationality champion Martin subtly points us in the right direction.

Those in the teaching profession take note. If we never present our students with such questions, perhaps we are spoonfeeding them too much, by only asking them to process easier, pre-digested problems. [AWKWARD/PREACHY? REWORD?]

Relevant quotes: sprinkle half a dozen of these throughout the blog?